- Solid State and Molecular Theory
- Any distinction between solids or molecules, or different flavors of "condensed matter" are artificial. The physical properties of any material can be predicted by solving one and the same Schrödinger equation, which is what quantum chemists and condensed matter physicists do using different approximations. The schism between physics and chemistry arises only from incompatible nomenclature and the fact that approximations good for atoms or molecules (used by chemists) fail at the continuum limit, and continuum approximations (used by condesed metter physicists) fail at the atomic or molecular limit. We seek for "molecular" or "atomic" trends in solids, and/or investigate bulk properties in small isolated molecules or clusters. Most of our projects deal with 3d transition metal atoms in different, solid or molecular, environments.
- Some research projects of solids, molecules, or both, are described below.
|
- Defects in semiconductors or insulators
- The isolated impurity in a semiconductor or insulators shares many features of a free atom, but at the same time it adopts properties from the surrounding bulk material. The bulk perturbs the impurity atom, and at the same time, the impurity perturbs the bulk. Despite the terminology, this problem is too hard for simple perturbation theories, and requires more heavy artillery.
- Assume the semiconductor host has (free electron or hole like) charge carriers. Can the wavefunction of such carriers around an impurity be described as small perturbations of the free-carrier like states, or are they trapped in bound small polaron states? This is theoretically quite challenging, as HF like theories tend to predict bound states, while local density approximations to DFT tend to predict perturbed host like states. Only one of these is correct.
- We employ self-interaction corrected functionals to DFT (see Lany & Zunger, Phys. Rev. B, 81, 205209 (2010)) to accurately describe carrier trapping on specific lattice sites vs. free-carrier states. Carriers trapped in polaron states can be released into free-carrier states by increasing defect concentration (see Bae, Raebiger, Phys. Rev. B. 94, 241115(R) (2016)).), or toggled from one type of state to the other by applying axial strain (see Bae, Raebiger, Phys. Rev. Mater. 2, 024402 (2018)).)
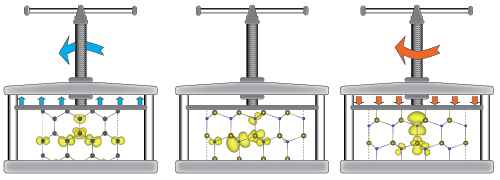
- Charge states, oxidation states, valence
- Assume an imuprity induces multiple bound states, each of which can trap electrons (or holes). The occupation of such traps is described in terms of oxidation numbers or charge states, but are such changes in occupation numbers really associated with integral changes in the local charge?
- Changing the occupation of an electronic orbital is never a small perturbation. Adding charge to a localized trap repels all the other electrons that initially were at that site, and removing charge has the opposite effect, which can be described as a self-regulating response that assures local electroneutrality. See Raebiger, Lany & Zunger, Nature 453, 763 (2008). Image below visualizes the self-regulating response by the charge density differences between different oxidation numbers.
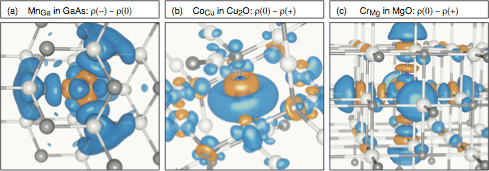
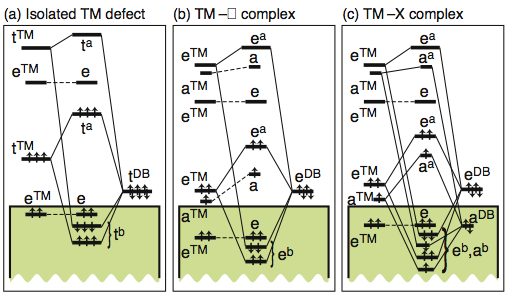
- Defect complexes
- Assume we have multiple defects close to one another. Can the electronic structure of such defect complexes be described by somehow superimposing the individual defect electronic spectra?
- There is no way to superimpose electronic spectra of defect complexes from isolated defect spectra. However, the above self-regulating response is quite useful to predict the perturbed wavefunctions of defect complexes! See Raebiger, Phys. Rev. B 82, 073104 (2010). Image below shows MO diagrams of different defect complexes in a tetrahedral III-V semiconductor.
- Quasi-1D chains embedded in semiconductors
- 3d impurities in semiconductor hosts tend to form pairs and clusters due to strong binding interactions, cf. molecules embedded in a solid. Via nonequilibrium growth, such bonding may actually drive the formation of complicated nanostructures inside the bulk. A simple illustration of quasi-1D chains of Cr atoms embedded in ZnTe is shown in the figure below.
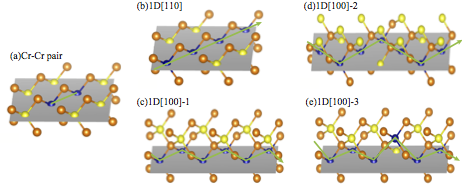
- Such quasi-1D chains may actually be more stable than simpler isolated clusters, and their stability and magnetic properties depend on the dimensionality and thickness of the chain. Moreover, the stability and preferred oriantation may be controlled by Fermi-level engineering via e.g. co-doping with other species. See Nakayama, Fujita, Raebiger, Appl. Phys. Express 6, 073006 (2013).
|
- Organic or inorganic?
- Both carbon and silicon have 4 valence electrons (as do Ge, Sn, and Pb),
but only carbon can form organic molecules.
Silicon does form polysilanes (similar to alkanes), but the unsaturated hydrides are completely different
from respective unsaturated hydrocarbons.
What's special about carbon, and why can carbon form a unique set of rigid, linear (polyunsaturated) hydrocarbon chains?
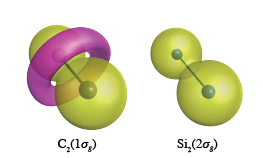
We carry out benchmark calculation of C2, Si2,
and their hydrides X2H2n,
and find that carbon has the propemnsity to alter the topology of
its core electronic orbitals when it forms unsaturated molecules.
For example, the C1s orbitals in C2 form a torus like ring around the bond center,
while the Si1s and Si2s orbitals in Si2 maintain their spherical like shapes, and topologies.
See Yoshida et al, Angewandte Chemie International Edition, 2018.
- Spin states and magnetism
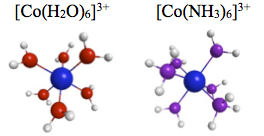
- Most of the time, 3d impurities in semiconductors or insulators are stable in their high spin state but also low spin states exist. Their stability is very sensitive to the computational method empliyed. This ligand field problem has been studied for decades, but is it even possible to quantify or define such ligand fields?
- Here, we romeve the bulk from around the 3d atom, and study octahedral cobalt clusters. This is the simplest model system that is well known to exhibit both high and low spin states, and these are (barely) feasible to calculate via heavy quantum cheimcal artillery. Our CASSCF calculations suggest that, indeed, ligand field theories are invalid! See preprint.
|
- Molecules adsorbed at solid surfaces
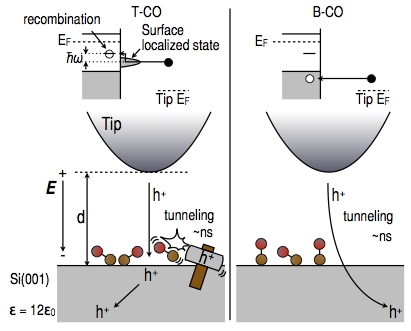
- The Si(100) surface is very reactive, and different molecules adsorb easily onto it. Our experimental collaborators have exposed pure Si(100) surfaces to CO molecules, known to stick to it with an adsorption coefficient close to unity, but nonetheless, STM images of these surfaces look like ones of pure Si(100) surfaces. Only after multiple STM scans do new bright spots appear, even though during such scans the system is not exposed to any new possible adsorbates.
- Our theory & experiment collaboration has shown that CO adsorbed to Si(100) in its stable configuration is invisible to STM. However, multiple scannings may change the absorption site to a metastable site due to an inelastic local heating mechanism (illustrated below). See Momose et al, J. Phys. Chem. C (2014)..
|
- Other ongoing projects
- In addition to the above described projects, we have many other activities, including but not limited to the following.
- Theory of diatomic molecules and small metallic clusters.
- Theory of magnetism, magnetic interactions, and chemical bonding.
- Metal-ssemiconductor interfaces, microscopic modeling of Schottky type interfaces; applications to photovoltaics.
- Binding of positrons in small molecules.
|
| © Hannes Raebiger, 2013-2018 |
|