SSMT CREW FLEET PROJECTS RECRUIT PAPERS

Gadolin Cluster computer is named after the Finnish scientist Johan Gadolin (not the fascinating magnetic element, which is named after the very same person). Gadolin did seminal work on rare earth oxides, and is acknowledged to be the first one to identify a rare earth element. He discovered yttrium, which is named after the town of Ytterby, from where samples of the peculiar oxide yttria were found. 10 Xeon 5570 8-core CPUs with 24 or 48GB each. InfiniBand network. Performance optimised for running VASP. Shared supercomputing facilities In addition to Gadolin, we use the supercomputer facilities offered e.g. by the Institute of Molecular Science (IMS), the Institute of Solid State Physcs (ISSP). 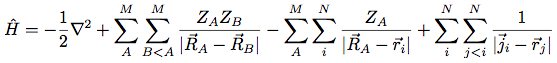Many-electron Hamiltonian The above many-body (electronic) Hamiltonian lacks analytical solutions for anything beyond 1-electron atoms, and must be solved numerically. We do this via two approaches: In the Hartree-Fock (HF) approximation, a single Slater determinant wavefunction is constructed, which is variationally minimized. This form of wavefunction naturally satisfies the Pauli exclusion principle, because two electrons with the same spin never spatially coincide (Fermi correlations). The problem here is that in HF, electrons with opposite spins may spatially coincide even though they should not (the Coulomb potential diverges; Coulomb correlations). The Coulomb correlations may be estimated perturbatively (MP2, MP3 and so on), or variationally. We mainly evaluate Coulomb correlationa variationally by constructing wavefunctions of multiple Slater determinants in Configuration interaction CI or multi-configuration (MCHF) calculations. We mainly use GAMESS for HF and post-HF (CI, MCHF, CASSCF) calculations. This is a local basis code, well suited for the calculation of isolated atoms or molecules. Density-functional theory (DFT) is a completely different approach, where the above many-electron Hamiltonian is mapped onto effective 1-particle "Kohn-Sham" equations. Here, the electron-electron repulsion of the full Hamiltonian (shown above) is approximated by an effective (local) 1-electron potential, usually based on approximations relying on the exact exchange energy calculated for the homogeneous electron gas. The problem in such local approximations is that electrons interact unphysically with themselves, leading to the self-interaction error. There are several approaches to try to cancel such spurious self-interactions; we use non-local potentials that receover the Koopmans' condition. We use the VASP for DFT calculations, which is a plane-wave code suited for periodic bulk calcualtions. We are active in the development of non-local potentials for both self-interaction and band-gap corrections. © Hannes Raebiger, 2013-2018